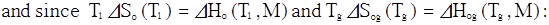STANDING ON THE SHOULDERS
OF A
VISIONARY GIANT:
RAYMOND F. BOYER
It took me more than 40 years to
fully realize the extraordinary vision that Boyer had in believing and pushing
forward, in his lectures and numerous publications, the importance of his TLL
transition in the upper amorphous melt, and
his Tg(U) and Tg(L) glass transitions in semi-crystalline
materials. Both concepts were truly at odds with the established models of the
amorphous state and of crystallization from the melt, at the time. Both
concepts still remain, 50 years later, almost totally forgotten; in the grand
library of the world knowledge, some would even rightfully say:
“who needs
that?”
This blog post #35 shows how to derive the existence of TLL,
and how to explain it. It also
introduces the dual and cross-dual phase concepts that are behind the presence
of the two Tgs in semi-crystalline polymers.
Thus, Dr. Boyer was right! TWICE!
This post is a
brief description of my steps which led to the explanations of TLL and
of the double Tgs.
Prof. R.F. Boyer inspired
me to question my own knowledge in the field of polymer physics.
The
1st time I met Prof. Boyer was at MIT in the spring of 1972 when he
came to give us a lecture on his 2 Tgs in polyethylene: Tg(L)
and Tg(U)[1].
I
already had heard of him from the classes I had attended at MIT, and of his
controversial views regarding the existence of his TLL transition
relaxation, located somewhere at ~1.2 Tg (oK) in the melt,
which he had coined the “liquid-liquid” transition[2].
After
his conference, I had the privilege to be invited, in the office of my
supervisor, to a one on one private conversation of an hour or so with him.
Needless to say, this meeting had a profound impact on me. Not only was Ray Boyer
a brilliant polymer physicist with an amazing memory capable of recalling and
quoting all that had been published and considered important in polymer physical
chemistry and physics in the previous 30 years, he was also engaging, kind and
witty, humble with a sparkling
intelligence that made me instantly like him.
The
2nd memory I have of Boyer took place in the summer of 1973 in
Midland, Michigan, where he held the position of Director of Corporate Research
at Dow. At a time when corporate research still blossomed from fundamental
science, I am sure that he and Dr. Turner Alfrey were responsible for my being
given the chance to live the experience of a summer job at Dow. Boyer continued
to expose and inspire me with his new ideas and with his list of remaining
problems to solve in polymer physics.
I almost exclusively focused on TLL,
since my PhD research involved a new understanding of the interactions in the
amorphous state[3].
I met Boyer’s wife and daughter, was invited to his place and even learned how
to clear away the nasty smell off a dog sprayed by a skunk! I remember the poor
dog in the bathtub being brushed with tomato juice all over its body!
And
then, I have a funny anecdote that came a few years after I had returned to
France; this happened at a time when Ray Boyer had paid me a visit in my
materials research lab in Ballainvilliers, near Orly airport, a place literally
in the middle of nowhere, surrounded by huge farmer fields growing potatoes or
who knows what else. We were invited for lunch at my home.
My car was a Renault
4L that I had bought for 500 Francs, i.e. less than 100 euros; a crusty white
little thing that had the merit to drive through shortcuts on tractors’ tracks
in the middle of muddy and slippery fields. Ray and I had started a passionate
discussion on some aspect of the TLL transition, as I was driving
through the fields, sliding here and there like on ice, not really paying
attention to the driving.
At one point I realized that I was the only one
talking, that Boyer was actually holding onto his seat with his two hands, his
mouth open, intensely watching the wipers making noise and swiping mud traces
on the windshield. It must have rained all night, or all morning, I also suddenly
realized. “Are you OK”, I asked him.
He looked at me and said, with a weird deep voice:
“How far are we going? Are you sure we will
make it?”.
These
same questions seem to have framed my whole research life: How far am I going
with my new ideas on interactions in physics? Am I sure I will make it?
It
was very promising yet surprising that a famous scientist such as Boyer showed
such a genuine interest in my work. However, I was obsessed by the implications
of the new ideas I was tossing in my head, and realized that my work had just
started: that I needed to dig, to think,
to learn…, yes, just learn and think…, intensely..,. and Boyer was a living
library to learn from (BTW did you notice the size of his forehead in the
Hall of Fame picture above…?).
So,
regarding my interest in Boyer’s controversial ideas, I was uncertain what to
think of it: what was the impact of TLL and of the double Tgs
on my own theoretical model of polymer interactions? Should
I discard these Boyer’s concepts…, like everybody else…, or did my model
explain them?... Should my model explain them?... What if Boyer was right and
my model did not explain them… (that
was the case of the classical models…)?
The
truth of the matter is that, in my lab, when I kept repeating Boyer’s
experiments and the analysis of his results (DSC, TSC, dynamic viscosity etc.),
TLL was there, not very pronounced, but there, for sure. When I
devised new ways to analyze the data (computerized double-shifting[4]),
TLL appeared when it was not discernable before, or even became more
prominent than before when it used to be a fuzzy signal. I published these findings: no reaction; the TLL
case was closed, Boyer had lost, Flory had won: no local order, no TLL,
period!
Then
history turned the pages: de Gennes and his reptation ideas became the new
paradigm to follow: forget Flory, forget TLL, move on, and, by the
way, there was no place for a TLL transition in the melt from the
stand point of polymer dynamics! If
reptation was right, no TLL, so move on!
Still,
in the back of my head, the real question remained: what was the meaning of TLL
and what was its impact on the properties of the melt? Did it affect
processing, for instance? Was TLL important? Was TLL the
David who will make fall the reptation Goliath?
I knew that the local order explanation
offered by Boyer was probably incorrect[5],
yet that Boyer could still be right that TLL was a real transition-
relaxation. I needed to understand it
with my new theory on interactions. But how?
Reader: a brief fast forward to
the present (it’s linked, you will see):
I authored a book, just published
by HANSER (introduced at the K-2019 show in Düsseldorf):
The Physics of Polymer Interactions. A Novel Approach. Application to Rheology and Processing.
You will encounter many references
to the TLL transition in this book, each time showing a strong manifestation
of its existence, in the middle of the melt temperature range above Tg,
very near where Prof. Boyer had envisioned and predicted it (~ 1.2 Tg).
This new evidence was obtained recently, using Rheo-Fluidizer processing
equipment that shear melts under vibration to trigger various non-equilibrium
states before they are frozen into pellets. The analysis of those treated
pellets showed a strong TLL under recovery conditions. TLL
was not only impossible to miss,
but it could also be manipulated by the processing conditions, changing the
vibration frequency or amplitude, or changing the pressure in the
Rheo-Fluidizer.
Yet,
you will not see a mathematical demonstration of what TLL is, in that
book. This QED and its explanation is given in Chapter 6 of another book which
I have just finished, whose tentative title is:
Application of the Dual-Phase and Cross-Dual-Phase model of Polymer
Interactions to the Understanding of Melt Rheology.
Now, let’s return to our post story:
TLL
is a real transition: QED.
Excerpts
from Chapter 6 of that new book follow:
...
After
a thorough description of the interactions for M > Mc in the
previous chapter, our objective, in this chapter, is to show that the
dual-phase approach also provides a better understanding of the interactions
for low molecular weight polymers (Mc
In particular, the current theories
of the melt liquid state have ignored, even vehemently opposed, the existence
of a "Liquid-Liquid transition", TLL, above the Tg of polymer
melts. The controversy has been introduced in the previous chapter in the case
of the M> Mc
data. We will now use a modified expression of the Vogel-Fulcher equation,
which we call the "Thermo-Vogel-Fulcher equation”, to show that TLL
naturally derives from it, demonstrating its fundamental aspect.
We also examine the rheological and
thermal analysis consequences of the existence of TLL and cite the
experimental evidence of TLL
exposed by Boyer and others, ignored by the current theoretical models of the
liquid state of melts, to show that this evidence may be interpreted and
derived from the dual-phase and Cross-Dual Phase aspect of the interactions in
polymers.
Everybody knows the famous
Vogel-Fulcher hyperbolic description of the temperature dependence of the
Newtonian viscosity, log ho:
(1)
Now,
let us define the Thermo-Vogel-Fulcher expression (TVF) of the Vogel-Fulcher (VF) equation:
(2)
.
T1 is a “Reference temperature” of the TVF equation; such a
reference state also appears in the WLF expression in its most general form.
The
changing of the reference state in the TVF equation and its consequence on the
value of DHo and DSo is
similar to the variation of the WLF constants C1, C2 with
the choice of the reference state, (T1, Logho1) in the WLF equation. The WLF constants are often quoted with
a reference state taken at Tg. (Eq. 3):
(3)
This
led Williams, Landel and Ferry to speculate that the C1g and C2g
constants of the WLF equation were universal constants [2]. We have challenged
such a claim in another publication [6], and it seems that most of the polymer
scientists, our days, concur. When the reference is switched to T1,
it is straightforward to find new WLF constants, in a way similar to what we
will do in the following to find the evolution of
DHo(T1,M) and DSo(T1,M) as
T1 and M vary.
Our interest is to choose T1
such that the free volume remains constant for the reference state,
as M varies, contrary to what is usually done when either T or M is
alternatively changed as the other variable is constant, as if the effect of these
two variables were independent. This is the main question raised and studied in
this book: is it justified to separate the effect of M and T on the
viscoelastic properties of polymeric melts?
Once the equations of DHo
(T1, M) and DSo (T1, M) are known, it becomes straightforward to compare their
values at constant free volume, i.e. at (Tg + A), where A is
constant, and Tg is a function of M.
In the TVF equation, T∞ is also a function of M. In other words, we need to
know both Tg(M) and T∞(M). This is given in Eq. (4):
(4)
where ao and a1, are determined by Differential Scanning
Calorimetry (DSC) at a constant heating rate, and
bo and b1 by Vogel-Fulcher fits of the Newtonian
Viscosity dependence on temperature. When T is expressed in oK, M in
g/mole, MAJESTE (UPPA, PhD thesis, PAU-France) has stated that:
(5)
ao= 371 a1=114,000
bo=321.4 b1= 83,000
Derivation
of the expressions of DHo(T1,M) and
DSo(T1,M).
We start by rewriting the TVF equation at 2 reference temperatures T1
and Tg:
(6)
We now combine the 2 expressions of log ho(T):
We find ks=B. the numerator in the Vogel-Fulcher equation (1)
In summary:
(7)
We will only deal with T1=Tg(M)+A
in this blog post.
Study of
the effect of M on DHo(T1,M) and
DSo(T1,M) at
constant Free Volume defined from Tg(M).
Instead
of comparing the parameters of the TVF equation for various M < Mc at constant T1,
we consider, in this section, comparing
the parameters at constant free volume A, where A is established with respect
to the Tg of the polymer factions, since, for M < Mc, Tg (M) is a strong function of M: T1= Tg(M)+ A.
From Eq.
7, we have:
(8)
When A is constant when M varies, the free volume, defined by (T1-Tg) remains constant .
We create
a set of values of DHA(M) at A given, using Eq. 4 to
determine Tg(M) and T∞(M).
We plot in Fig. 3 DHoA vs 1/M at constant A for various
values of A varying between A=23 oC and 93 oC. We
see in Fig. 3 that straight lines visually pass through the data, and the
linear regression confirms that the linearity is rather good (last column of
TABLE 2). TABLE 2 gives the Intercept
and the slope of the lines in Fig. 3, when A varies. What is interesting is
that the slope starts from a positive value at T1=Tg (A=0), decreases as A increases, flattens out to 0 across all
values of M for A approximately equal to 70 oC, and becomes negative
as A continues to increase. For reasons
which will become apparent in the following, we will associate this peculiar
temperature T1 that makes DHoA
remain constant (to approximately 2600 in Fig. 3) across all M when the free
volume is set at A~70 oC, as the TLL temperature of Boyer, the liquid-liquid transition. This means that the state of the melt at that
particular temperature is an iso-free-volume state with also a constant Thermo-Vogel-Fulcher Enthalpy, DHo: an
iso-free volume-iso-enthalpic-sate, a unique situation as M and T1
vary.
A INTERCEPT SLOPE R2
0 5213.46 14490364 A →0
23 3806.02 677647.25 0.998
46 3066.31 188407.88 0.9989
70 2587.606 -39.6049 0.9768
93 2284.95 -74180.24 0.9995
TABLE 2
Results
of the regression lines in Fig. 3 of DHoA vs 1/M at A constant. A varies from 0
(Tg state) to 93 oC in this
plot. PS data from Majeste [6].
Fig. 3
Finding the reason for the TLL transition.
PS Dynamic
data of Majeste[6]-DHoA vs 1/ M at various A.
The TLL(M) is the temperature corresponding to the
0 slope, i.e. for A~ 70 oC. TLL
is an iso-free volume-iso enthalpic state. Graphically, we found :
TLL(M) =Tg(M)+70.5 oC for monodispersed PS with M < Mc
Let us now find the mathematical
expression of DHLL and ALL derived from the Thermo-Vogel-Fulcher
expression of DHA(T1,M) at free volume constant T1=Tg+A
(9)
Numerical Application (Majeste’s data
PS monodispersed M < Mc)
(10)
B=703.5571; ao=371 oK, a1=114,000; bo=321.4
oK, b1=83,000
Therefore:
(11)
ALL= 70.441 and DHLL= 2587.275
confirming
the values found empirically in Fig. 3.
In other
words, when T1=Tg+ALL, regardless of the value of M, DHLL=2587.275=constant.
The TLL is an iso-free volume and iso-enthalpic state of the melt,
a very unique situation.
In conclusion, we have
demonstrated the presence of the TLL
transition by “observing’ the variation of the thermodynamic terms of the
Thermo-Vogel-Fulcher equation with M via an observer T1, which we
define to keep the free volume constant across the values of M, when M varies.
We saw that TLL
corresponds to the value of T1
that makes the Thermo-Vogel-Fulcher Enthalpy constant as M varies, equal to a
characteristic of the melt that we call DHLL.
We derived several equations linking the state of the melt, characterized by
its value of DHA(M,A), DSA(M,A), to
the state of the melt at TLL:
DHLL, DSLL=DHLL/TLL, and we
saw that the free volume at TLL,
ALL, is constant for all values of M.
In
the next 50 pages of the book's chapter 6 (not
expanded in this blog post), it is shown how the presence
of TLL
influences the rheology of the melt, and is not a “mathematical
transition” due to the use of an observer. The reasoning is that since the free
volume above and below TLL
are different, in the sense that some transition occurs at TLL that
modifies the mechanism that generates the free volume, the Newtonian viscosity
temperature dependence must be affected when crossing the TLL
transition. Consequently, it must be necessary, when performing a regression
analysis of Newtonian viscosity-temperature data, for a given M, to distinguish
two regions: the one below TLL
and the one above TLL,
and we should obtain different parameters for, say, the regression of the
Vogel-Fulcher equation, Eq. (1) applied to these 2 temperature regions.
Also, in this same chapter 6, the
crucial impact of TLL in determining the melt structural differences
below and above TLL is quantified: I
quantified the amount of change of free volume at TLL and also the
amount of enthalpy change at TLL. I explained, and verified what I
had found experimentally: why shear-thinning and the time-temperature shift
factors are different below and above TLL and the impact this has on
the instability of the melt, leading to “smart processing” capabilities (this
is covered in chapter 8 of the Hanser green book pictured above).
In summary, Boyer was right concerning the existence of TLL.
He
was also right when he intuitively insisted on its physical importance. Yet, he was wrong in his view that its cause
was linked to a local order explanation, meaning something reminiscent to what
initiates crystallization. No, the restructuration of the free volume at TLL for M < Mc is linked to the
coupling between the compensating driving forces of the dual-phase model:
[(b/F) ↔ (c,g,t)], a very different reason than a local order explanation.
The
Dual-Phase [b/F ↔(c,g,t)] interpretation of the TLL
transition.
We
suggest that the TLL
manifestation is due to the duality of [b/F ↔(c,g,F)]. We further suggest that
the TVF functions,
DH(M,T)
and DS(M,T),
reflect the state of the duality.
The
b/F transition controls the nucleation and growth of the b-grains, and their
stability, which is a function of the conformation of the conformers
participating in the b-grains, itself controlled by the (c,g,t) kinetics. When
the thermal energy (kT in the Boltzman’s statistics) evens out the probability
to form or melt b-grains, the existence of the dual density fluctuation
dissolves in the thermal agitation, releasing the free volume that matched the
density difference between the F and the b-conformers. The F and the b-conformers become locally undistinguishable.
Instead of calling this process “the melting of the b-grains”, we prefer to see
it as a delocalization of the b-grains, referring to the impossibility to
localize the b-grains on the macromolecules. The b-grains melt and reform at
different places and with a rate faster than the frequency of observation. One
could easily conclude that TLL
is the state where the dual-phase physics, modulated by the Grain-Field
Statistics, intercepts and fuses with the classical “homogeneous” phase
physics, the arena of the Boltzmann’s statistics. Notice that the b-grains
continue to form above TLL,
yet they are delocalized, hence the presence of the b-grains and the absence
of the b-grains is locally indistinguishable. This delocalization results in an
increase of the apparent free volume.
At
the same time, the increase of free volume from within the macro-coil allows a
better inter-penetration between adjacent coils, translating into more
bond-sharing of the 2nd kind, or even of a higher kind, in the
composition of the b-grains; as a result the entropy increases (the macro-coil
radius expands a bit). The enthalpy
continues to increase because the number of conformers, and thus of the
formation of new b and F conformers, increases with M: this is just a scaling
effect.
In summary, for T >TLL, the
melting of b-grains of the 1st kind, as TLL
increases, releases the chain into more reconfiguration options within a
macro-coil, not only slightly expanding it, but also creating new
(indistinguishable) b-grains, increasing their number as the chain length
increases, and favoring their contact sharing with adjacent chains: we assume
that this mechanism may be the reason for the increase of entropy for T> TLL
for points 7-10. (not shown in this post). We will return to this issue in Chapter 7 of the book.
When
T < TLL,
for M > Mmc,
there is not enough thermal energy “to melt” and delocalize the existing b-grains and their free volume
environment: the rate of formation of the (localized) b-grains wins over their
rate of dissociation, yet this happens by a mechanism of growth of the b-grains
within the macro-coil, not by increasing their numbers with other chains; this
is perhaps why one observes a decrease of the entropy at constant DHLL, by
plateau-increments such as 4-5, then 6,7, then 8-10 for the blue dots in Fig.
30 (not shown in this blog post).
Thus my 1st conclusion
of this post:
Boyer was right regarding the existence of TLL in the upper
melt, although for the wrong reasons.
The 2nd
vision of Boyer: the two Tgs in semi-crystalline polymers. Was Boyer
also right?
Not only was I inspired by Boyer to
uncover the mystery behind the TLL transition, but I recently (5
years ago) also felt driven to understand the two Tgs of
semi-crystalline polymers envisioned by Boyer.
The question
that drove me to undertake this research was even more general: Is the Dual-Phase and Cross-Dual-Phase model
applicable to crystallization?
But first,
why do some melts crystallize while others remain amorphous? This should have a
simple answer from a dual-phase amorphous model perspective, even if I
considered myself primarily focused on the amorphous phase. If we had two types of amorphous phases,
shouldn’t this have an effect on the way the melt crystallizes?
Crystallization,
obviously, is an important research topic which requires a lot of dedication
away from the study of the amorphous matter. But crystallization is generated
from the amorphous state: I needed to get myself involved!
I started my own
inquiry by studying the influence of entanglement stability on the crystallization
process, which led to several lectures and Video Clip Lectures. I published in 2013 a short
paper on crystallization from the melt along those lines entitled:
Crystallization Kinetics for the Split
Dual Phase Model of the Amorphous State of Polymers[7]
The
reception of this paper by my peers has not stopped astonishing me: it has
become the most read paper of the few I have posted on Research Gate, with more
than 2,700 reads in 3 years! This interest pushed me to become more involved in
determining whether my model of duality-cross duality could help tackle
crystallization.
I can only say that the concept of crystallization emerges
naturally from the treatment of the amorphous state and its dual-phase or
cross-dual-phase structure. When conformers with the same stable
conformation create the equivalent of a b-grain, it becomes the nucleus for
crystallization growth. I call it the st-t (stabilized-trans) conformation
state, the most stable state achievable. For certain polymers, the classical
semi-crystalline polymers, that state is preponderant and easily accessible;
for other polymers, it not stable (amorphous polymers).
Therefore, in my new approach to crystallization, I treat
nucleation as a process that allows to pump or release trans conformers from/into
the global system Grain-Field statistics: it’s a competing mechanism to b-grain
formation: a new duality.
Another idea emerged from this research: to treat crystallization
like a cross-duality of the duality [b/F ↔(t, cgf, st-t)]. With that
perspective in mind, the crystallization dynamics is treated by analogy with
the dual-phase/cross-dual-phase split to explain the formation of
entanglements. In the case of the dual-phase-cross-dual-phase compensation, the
split allowed the formation of two types of crystals: the micelle type (the
M-phase) and the spherulite type (the S-phase), hence two types of amorphous
phases, characterized by their Tg(M) and Tg(S), which I
associate with Boyer’s Tg(L) and Tg(U).
In this new approach,
crystallization is the result of a competition at two cross-levels: the
formation of b-grains within both the S and M phases, and the compensation
between the S and M phases. The new model can be quantified by the same equations of the
Grain-Field Statistics that drive the interactions between conformers to lead
to entanglements.
The idea explored is that the same statistical phenomenon that
generates “entanglement” when M increases, - a duality that triggers a
cross-duality to minimize the dissipation energy of the global system-, is also
at work to produce the 2 amorphous phases, the S and M phases that are themselves
dual-phase-coupled with the 2 types of crystalline phases, the S and M crystal-phases!
The 2nd conclusion
of this post is that Boyer was also right regarding the presence of the Tg(L)
and the Tg(U) in semi-crystalline polymer melts.
Now, this 2nd aspect of my Boyer’s inspired research
might have broader consequences, touching areas other than those I initially
considered:
-
The effect of extremely low dilution of a component on the
structure of a liquid (isn’t this the current problem challenging the
scientific basis of homeopathy?).
-
The Dual-Phase and
Cross-Dual-Phase coupling of the electromagnetic field and the gravitation
field, and its consequence in understanding the time-space duality and the
time-space-inertia cross-duality?
The organization of the interactions into M and S cross-dual
phases, contemplated for the crystallization from the amorphous phase of
polymers, may look like a general idea applicable to all kinds of interactions,
and, provided it can correctly be mathematically modeled, I suggest that it is.
Simplicity hides itself by way of splitting and “folding” dual-phase solutions
of interactions, creating a ladder of entangled systems operating at
multiplexed levels; this makes the interactions look more complicated than they
actually are! The cradle for this
boundary-less dynamic interlocked network is the electromagnetic field, the
alpha-layer: the field without inertia, the medium that interconnects it all
after birthing it all.
I dedicate my findings regarding the QED TLL and the 2 Tgs in semi-crystalline polymers to the memory of Prof. R.F. Boyer (1910-1993), this visionary giant who guided my1st steps in this field.
“ Eh, Ray, despite my crusty car and the bad weather conditions, did we not make it?
POST-SCRIPTUM.
A new book presenting a dual-phase and cross-dual-phase approach to nucleation and crystallization under dynamic conditions is in the works: “The Dual-Phase and Cross-Dual-Phase Approach to Crystallization in Polymers (writing finished in 2020?).
REFERENCES
1. Raymond F. Boyer (1973), “An
apparent double glass transition in semicrystalline polymers”, Journal of
Macromolecular Science, Part B, Phys., 8:3-4, 503-537, DOI: 10.1080/00222347308201635
2. Raymond F. Boyer (1963) “The Relation
of Transition Temperatures to Chemical Structure in High Polymers”. Rubber
Chemistry and Technology: November 1963, Vol. 36, No. 5, pp. 1303-1421. https://doi.org/10.5254/1.3539649
2a. S.J. Stadnicki, J.K. Gillham, and
R.F. Boyer, J.Appl. Polym. Sci., 20,1245(1976)
2b. J.K. Gillham and R.F. Boyer,
J.Macromolecular. Sci., Part B, Phys.,13,497 (1977).
2c J. K. Gillham, Torsional
Braid Analysis (TBA) of Polymers, Developments in Polymer
Characterisation—3, 10.1007/978-94-009-7346-6_5, (159-227), (1982).
[3] Jean Pierre Ibar, “ A Theory for the Properties and the Behavior of Polymeric Materials”, June 75.
[4] J.P. Ibar, (1981) “Non-Newtonian flow behavior of amorphous polymers in the T>T g temperature range: A new analysis of the data according to the “double-shift” procedure”, J.Macromol. Sci., Part B, Physics 19:2, 269 308, DOI: 10.1080/00222348108223943
[5] This does not mean that crystallization and/or the tendency to crystallize does not affect TLL: it does, but local order is not responsible for TLL in my explanation of it.
[6.] J.C. MAJESTE (UPPA, PhD thesis,
PAU-France).
[7] J. P. Ibar (2013) Crystallization Kinetics for the Split Dual Phase Model of the Amorphous State of Polymers, Journal of Macromolecular Science, Part B: Physics, 52:7, 950-963, DOI:10.1080/00222348.2012.746571 To link to this article: http://dx.doi.org/10.1080/00222348.2012.746571
Jean Pierre Ibar
October, 2019