Rheo-Cooling applied to Plastics.

Rheo-Cooling applied to Plastics.

     As the primary use of a mold is to shape material into an object, not to cool it, conventional molds are not designed to apply specific cooling treatments to materials, although they are implicitly used as heat transfer agents to solidify the material.  When Rheo-Cooling development is aimed at implementing specific cooling treatments and the material cooled is a plastic in a mold, this implementation has been called “Rheomolding”.

Rheomolding based processes use rheology principles to vary the value of physical transitions (T_g, T_m) as the material temperature decreases to cross them at any given speed. Take a rubber, for instance: its modulus depends on the value of (T-T_g) where T is the temperature and T_g is the glass transition temperature. T_g is itself function of pressure and of the frequency and amplitude of a vibration if such a mechanical force is exerted on it (shear or pressure vibration).  

     The figure below shows the pressure dependence of T_g for Polystyrene. T_g varies by 32 ^oC/Kbar. This means that if one applies a pressure variation of 1 Kbar per sec, for instance, one obtains a Rheo-Cooling rate of 32 ^oC/ sec, i.e. 1920 ^oC/min!. This is not achievable by conduction, especially for a bulk material, yet Rheo-Cooling gives you such possibilities (see the previous blog: Rheo-Cooling 1 l of water in less than 5 sec)!

     Fig. 1 shows that the rate of cooling influences the state of the glass once the T_g is crossed. We can measure the specific volume at different temperatures while the material cools: the break and the change of slope corresponds to the T_g; Fig. 1 shows that if the material is quenched, its T_g is higher and the glass produced is in a state of non-equilibrium which is more pronounced. 

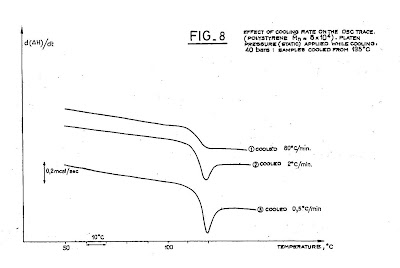
     In fact one can demonstrate that the material cooled faster is in a different state of non-equilibrium by studying the DSC trace obtained by heating a piece of it after it has cooled to room temperature. This is shown in the following figure (“Figure 8”). 

     One sees that the “fast cooling”, at 80 ^oC/min produces on heating a characteristic DSC trace of quenched glasses: there is only a drop of the baseline occurring at T_g, no peak visible. For the 2^oC/min cooling rate, a peak is visible, indicating an overshoot of the heat capacity before the liquid state is reached. This peak is more pronounced for the even smaller cooling rate of 0.5 oC/min.

     OK, we have in hand a nice way to know if the glass was slowly cooled or “quenched” during its solidification:  we can run a DSC scan on it and determine the size of the peak at Tg.  This can be very useful to characterize the glasses formed by Rheo-Cooling.  

     What other physical parameter can we think of to alter the value of phase transitions, besides pressure?

    Frequency maps were popular in the 70s which provided the variation of the phase transitions with frequency (T_a, T_b etc.). An example is shown in the figure below for the T_a transition of Polystyrene. 

     The T_a transition is the mechanical representation of T_g. What this figure says is that T_g is dependent on the value of the frequency when the material is oscillated, like it is dependent on pressure. The Frequency map shows that the value of T_g varies by 49 ^oC when the frequency varies from 10^-1.5 Hz (the point corresponding to 1000/T = 2.725) to 10⁵ Hz (the point corresponding to 1000/T = 2.4). In other words, one can sweep frequency to increase or decrease at a given rate and this will correspond to Rheo-Cooling or Rheo-Heating effects. For instance, one can choose to vary linearly the logarithmic of the frequency to simulate cooling rates and produce various types of non-equilibrium states for the glass formed under such conditions.

     In the video shown below I present an equipment which was built to apply variable  frequency ramps and high amplitude hydrostatic oscillations during cooling of a plastic in order to implement various kinds of Rheo-cooling treatments across the T_g of that plastic.

     Frequency is swept from low to high value as temperature decreases, raising the value of T_g at any chosen rate. The amplitude of the oscillation is also increasing during the same time. These oscillations are continued until the material temperature is reduced to a level where frequency effects are no longer required to maintain product integrity (~ 20 ^oC below T_g).       In the video we hear the frequency increase from 1 Hz  to 3000 Hz. The sample is a Polystyrene disk confined in a mold at room temperature, heated to an initial temperature where it is a viscoelastic rubber, pressurized in the mold to an initial pressure which can vary between 500 and 10,000 PSI, the pressure being capable of oscillation of 0 to 100% in excursion. The apparatus has cooling channels and heating cartridges disposed in the mold to control the rate of cooling by passage of refrigerant fluids, such as water, a mix of glycerol and water, or compressed air. The lower mold half is attached to a vibrating table which imposes the pressure excursion to the plastic disk through an accelerometer. The upper mold half is fixed and connected to a pressure cell. A pneumatic air piston, shaped like a flat inflatable disk, transmits the average hydrostatic force while the electromagnetic shaking table exerts the pressure excursion.

     We see in the video the different elements composing the Rheomolding apparatus set up: watch the technician take the machine apart, once the Rheo-cooling experiment is done, in order to separate the two mold halves and extract the treated polystyrene disk.  This treated sample is submitted to a series of tests to determine the difference in properties between references (purely static runs) and “Rheomolded” conditions. We characterized the thermal, mechanical and dielectric properties of these materials. 

     We run DSC tests  for the treated samples to reveal what type of non-equilibrium states were achieved by Rheo-cooling or Rheo-heating while the glass was being cooled by conduction. The figure below (“Fig. 7”) tells the story for two treatments which are, each time, compared to a reference sample obtained under the same cooling conditions , except without any frequency sweep in the mold ( “no vibration”). 

Treated sample 1:

The REFERENCE curve for treated sample 1 is the 2^nd curve from the top. It shows a typical drop off of the Heat Flow baseline at T_g, characteristic of a fast cooled sample (80 ^oC/min). The top DSC trace, however, corresponding to the TREATED sample, is very strange: the DSC trace displays a strong peak at T_g, a characteristic of a very slowly cooled specimen, but, noticeably, the baselines for the melt and for the glass are the same, unlike for slowly cooled samples (see above). This is as if there was no longer a difference in the Heat Capacity below and above T_g: DC_p(@ Tg)=0!

Treated sample 2 (lower two traces):

The REFERENCE is, again, typical of a fast cooled sample: no peak at T_g. The treated sample is very different from the reference sample cooled identically but with no vibration during cooling. The endothermal characteristics at T_g are more complex for the treated than for the untreated sample. In particular, the endotherm at T_g is broader for the treated sample, extending over 40 ^oC range above T_g. Then, the baseline seems to be shifted upward by an exothermic wave, in a way similar to what happened to the treated sample 2.  At the end, up in the high melting region, the heat capacity seems to extrapolate from the solid region, similarly to  what was seen for treatment 1.

     In conclusion, it appears that the sample which has been Rheo-Cooled had thermal characteristics at room temperature (after the treatment) which could be extrapolated from the liquid region where it is known that the polymer is at equilibrium. This would mean that the treated sample behaved below T_g like a sample which had reached equilibrium, i.e. like a specimen which has been extensively annealed.

     The other possibility that comes to mind is to challenge the fact that the liquid region, above T_g, is at equilibrium; in other words, Rheo-Cooling can create non-equilibrium liquid states.

    It took me to build another machine, the Rheo-Fluidizer, the subject of recent publications, to prove that the liquid state could, indeed, be brought out of equilibrium with respect to its state of entanglement.

     This brings us to the Split-Dual-Phase model of entanglement, which I have discussed already in previous blogs and lectures.

    Something is clear to this author: melt manipulation such as Rheo-Cooling and/or Rheo-Fluidification, or any combination thereof, gives us formidable new tools to prepare new plastics; and, for a change,  this is not based on what chemists can do: synthesize millions of new molecules and their blends; but rather it is because a new understanding of the physics of the interactions between the macromolecules opens a wide new door to the way they can be processed:  the age of Smart Processing can proceed!

PS  

I will provide in a separate seminar the processing details for the experiments described in this blog.